패리티비트와 해밍코드

오류 정정

반도체 기억장치 시스템은 오류가 발생할 수 있다. 이러한 오류는 하드 결함과 소프트 결함으로 구분될 수 있다.

하드 결함이란 영구적인 물리적 결함으로, 기억 소자가 안정되게 데이터를 저장할 수 없어서 0또는 1로 고정되어 있거나 0과 1사이의 값을 불규칙하게 가지는 것을 말한다. 하드 오류는 열악한 환경에서의 남용, 제조상의 결함, 혹은 마모에 의해 발생한다.

소프트 결함은 기억장치의 내용이 일시적으로 변경되는 가벼운 오류로서, 전원공급장치의 결함이나 알파 입자가 원인이 된다. 이러한 문제는 방사능 붕괴의 결과로 발생한다.

이러한 오류들을 검출하기 위해서 대부분의 기억장치 시스템들은 오류를 검출하고 정정하기 위한 논리회로를 포함하고 있는데 이 방식에 사용된 코드가 이번에 알아볼 패리티 비트와 이를 응용한 해밍 코드 이다.

패리티 비트

패리티 비트(Parity bit)는 정보의 전달 과정에서 오류가 생겼는 지를 검사하기 위해 추가된 비트이다. 문자열 내 1비트의 모든 숫자가 짝수 또는 홀수인지를 보증하기 위해 데이터의 각 문자에 1비트를 더하여 전송하는 방법으로 2가지 종류의 패리티 비트(홀수, 짝수)가 있다.

• 짝수 패리티 : 짝수 패리티는 전체 비트에서 1의 개수가 짝수가 되도록 패리티 비트를 정하는 것이다.
• 홀수 패리티 : 홀수 패리티는 전체 비트에서 1의 개수가 홀수가 되도록 패리티 비트를 정하는 것이다.

위와 같은 경우로 오류를 검출할 수 있지만 패리티 비트는 오류 발생 여부는 알 수 있지만 오류를 검출할 수 는 없다. 즉, 어떤 비트가 오류비트 인지 알 수 없는 것이다. 또한 완벽한 에러 점검 방법은 아니라고 할 수 없는 것이 전송 중 두 비트가 동시에 에러가 나는 경우는 잡아낼 수 없기 때문이다. 하지만 PC내에서의 전송은 이러한 극히 적다고 간주되며, 대형 컴퓨터 시스템들에서는 패리티 체크를 위해 비트 3개가 할당되기도 한다.

해밍 코드

해밍 코드(Hamming Code)는 수학자 리처드 해밍이 1940년대 말에 벨 연구소에서 개발하여 1950년에 펴낸 저서에 소개되었는데, 그의 이름을 따서 해밍코드라고 명명되었다. 해밍코드는 데이터비트에 몇 개의 체크비트가 추가된 코드로, 기존의 체크 비트들은 에러가 있다 없다 정도만 확인할 수 있었던 반면, 해밍코드는 에러비트의 위치까지 알수 있으며 정정까지 가능하다.

해밍 코드는 코드 생성 -> 오류 검출 -> 오류 수정의 단계를 가지고 있다.

이 단계를 설명하기 위해 전송하고자 하는 데이터를 88이라고 하자. 이 데이터는 이진수로 $1011000_{2}$을 갖는다.

해밍 코드: 코드 생성 단계

여기서부터는 흐름을 한번 놓치면 매우 어려워질 수 있기 때문에 집중해서 한줄 한줄 살펴보도록 하자.

해밍 코드를 생성하기 위해 데이터와 합칠 체크비트가 필요한데, 이 때 필요한 체크 비트의 갯수는 아래의 공식을 따른다.

$2^{p}\geq d+p+1$

• d : 데이터 비트
• p : 체크 비트

$1011000_{2}$은 데이터 비트가 7비트이다. p는 최소 4가 되어야 하므로 필요한 최소 체크 비트 수는 4개가 되는 것이다.

이 체크 비트를 데이터 비트 사이에 끼워 넣는 방식은 Little Endian방식과, Big Endian 방식이 있다.

• Little Endian 방식 : 오른쪽에서 왼쪽으로 $2^{n}$ 자리수에 넣는다.
• Big Endian 방식 : 왼쪽에서 오른쪽으로 $2^{n}$ 자리수에 넣는다.

여기서는 Little Endian을 방식을 사용하여 해밍 코드를 구성해보도록 하겠다. 그렇게 하면 체크 비트4개를 아래와 같이 넣을 수 있다.

그 후, 원래 집어넣고자 하는 비트를 사이사이에 채워 넣어주면 $1011000_{2}$ 는 아래와 같이 들어가게 된다.

이후, 1의 위치를 확인한 뒤에 이 위치를 이진수로 변경해 준다. 위의 그림을 보면 1은 11, 9, 7번째에 있어서 $1011_{2}$, $1001_{2}$, $0111_{2}$이 된다.

이제 이 나온 숫자를 XOR 계산을 해준다. 그럼 아래와 같이 $0101_{2}$이 나오게 되고 이 비트를 차례로 체크 비트 위치에 넣어주면 아래 그림과 같이 된다.

위의 표의 해밍 코드가 오류가 없는 해밍 코드라고 볼 수 있다.

해밍 코드: 오류 검출 단계

이제 위와 같이 전송된 해밍 코드가 어떻게 오류를 검출하는지 알아보도록 하자.

$10101001001_{2}$ 이 $10101001101_{2}$로 잘못 전송되었다고 가정해 보자. 검출 방식은 짝수 패리티 방식을 사용하자.

$P_{1}$ 부터 $P_{4}$ 까지는 $2^{n}$개씩 영향을 주게 되는데 아래 그림과 같이 나오게 된다.

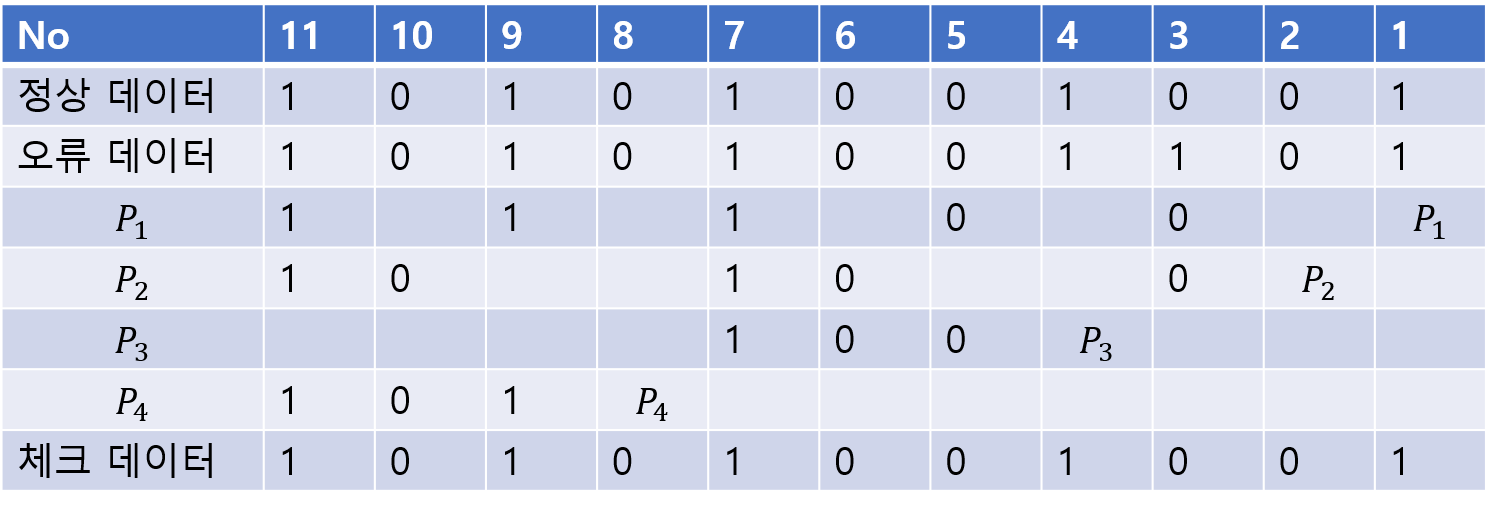
$P_{1}$은 1비트씩, $P_{2}$는 2비트씩 $P_{3}$는 4비트씩 $P_{4}$는 8비트씩 패리티 비트 검사를 하기위해 각각의 자리를 사용하게 된다.

이렇게 $2^{n}$개씩 자리를 정하는 방식을 공식으로 쓰기도 하는데 다음과 같이 표로 나타낼 수 도 있다.

자리번호 수만큼 이진수를 써보면 위의 표처럼 나오는데 이때 각 자리의 1의 위치가 패리티 비트 검사를 수행할 비교 자리가 된다.

$2^{0}$ 즉 $P_{1}$을 결정할 수의 자리는 $2^{0}$에서 1이 위치한 1, 3, 5, 7, 9, 11자리가 비교 자리가 된다.

이런 식으로 $2^{n}$까지 수행하면 아래와 같은 자리 비교표를 가질 수 있다.

이제 이 방식을 써서 짝수 패리티비트 검출 방식으로 각각의 수를 구하면된다.

• $P_{1}$칸은 1이 4개이므로 $P_{1}$의 자리는 0이 되어야 하는데 $P_{1}$의 자리는 1이어서 오류가 검출 된다.
• $P_{2}$칸은 1이 4개이므로 $P_{2}$의 자리는 1이 되어야 하는데 $P_{2}$의 자리는 0이어서 오류가 검출 된다.
• $P_{3}$칸은 1이 1개이므로 $P_{3}$의 자리는 1이 되어야 하므로 오류가 아니다.
• $P_{4}$칸은 1이 2개이므로 $P_{4}$의 자리는 0이 되어야 하므로 오류가 아니다.

이처럼 $P_{1}$과 $P_{2}$에서 오류가 검출되어서 위의 코드는 오류임을 알 수 있다.

해밍 코드: 오류 수정 단계

위에서 말한 것처럼 $P_{1}$과 $P_{2}$의 비트가 오류임을 알 수 있는데 이 위치 값을 더하면 1+2 = 3이 된다.

따라서 3번째 자리 수가 오류 임을 알 수 있게 되어 1을 0으로 고치면 된다.

해밍 코드 장단점

위의 과정처럼 해밍 코드는 에러 검출과 수정을 위해 많은 체크 비트가 필요하지만, 데이터 송수신시에 오류데이터가 전송 되었을 시, 데이터를 재 요청할 필요가 없이 스스로 에러 코드를 수정할 수 있다는 장점을 갖고 있다.

이외의 오류 검출 방식

이외에도 오류를 검출 할 수 있는 여러가지 방식이 존재한다. 여기서는 간단하게 어떤 것들이 있는지 나열하도록 하겠다.

• 반복 부호
• 순환 중복 검사(CRC)
• 블록합 검사(BSC)
• 체크섬(Checksum)
• 암호학적 해시 함수
• 전방 오류 정정

나올 수 있는 면접 질문

• 패리티 비트란 무엇인가요?
• 패리티 비트는 어떻게 오류를 검출하나요?
• 해밍 코드의 장단점은 무엇인가요?
• 해밍 코드의 오류 검출 및 오류 수정 과정은 어떻게 되나요?

참고 url

• 컴퓨터 시스템 구조론 10판
• 패리티 비트 - 나무 위키
• 에러 검출과 에러 정정 - 위키피디아
• 해밍 코드 한방에 부수기 - Youtube

기여자

_{Kyun Heo}
📦